Industry Mentorship Program - Neural Options Pricing
The team for the industry mentorship programme received mentorship from a quant professional, and researched the usage of Deep Neural Networks for the pricing of (non-vanilla) options:
Broad Methodology
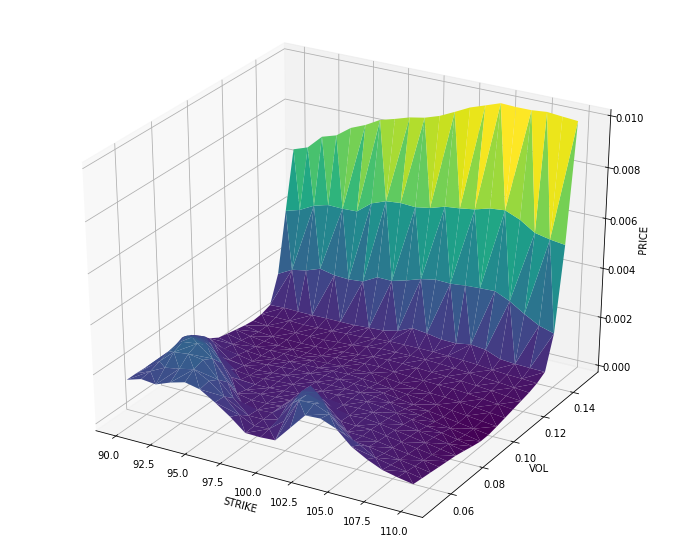
A grid of options pricing parameters is used as inputs
$$\mathbf{X_{i}} = (S, K, t, r, \sigma)^{T}$$
Spot price, Strike price, time to maturity, interest rate, implied vol
The price Black Scholes is used as a target
$$y_{i}=\mathbf{f}(X_{i})$$ where \( \mathbf{f} \) is the Black-Scholes formula
And a Deep Neural Network is used as an estimator and Mean-Squared Error is used as a loss Function:
$$\mathbf{\hat {f}} = argmin \frac{1}{N} \sum (y_{i} - \tilde f(X_{i}))^{2}$$
where \( \mathbf{\hat {f}} \) is the Deep Neural Network architecture with the lowest out-of-sample MSE
This approach is then extended to non-vanilla options, such as Barrier and Rainbow options.
22/06/2020